支持向量机(Support Vector Machine)的求解通常是借助凸优化技术。
间隔与支持向量
给定训练样本集$D={(x_1,y_1),(x_2,y_2),…,(x_m,y_m)},y_i \in (-1,+1 )$ 分类学习最基本的思想就是基于训练集D在样本空间中找到一个划分超平面,将不同类别的样本分开。SVM就是帮助我们寻找到众多划分超平面中最符合的。
怎样定义符合这个指标呢,作为分类问题,训练中能够尽可能划分出不同类别的样本是基本,然后在测试集中也能表现出来很好的分类能力,对未见示例泛化能力最强。在训练中表现的就是对训练样本局部扰动容忍度最高。
公式表示
划分超平面可以用此式表示:
$\vec{\omega}^T \vec{x} + b=0$
其中$\vec{\omega}=(\omega_1;\omega_2;…;\omega_d)$为法向量,决定了超平面的方向;b为位向量,决定了超平面与原点之间的距离。
样本空间中任意点到超平面x到超平面$(\vec{\omega},b)$的距离可写为:
$r=\frac{\mid\vec{\omega}^T \vec{x}+b\mid}{\mid\mid \vec{\omega}\mid\mid}$
设置函数:
$\omega^T x_i + b \geq +1 , y_i= +1$
$\omega^T x_i + b \leq -1 , y_i= -1$
简化两个式子:
$y_i(\omega^T x_i +b) \geq 1 , i=1,2,…,m$
这个是之后式子的约束条件
距离超平面最近的几个训练样本点使得上面的不等式等号成立,它们被称为支持向量(support vector),两个异类支持向量到超平面的距离之和称为间隔(margin)
$\gamma = \frac{2}{\omega}$
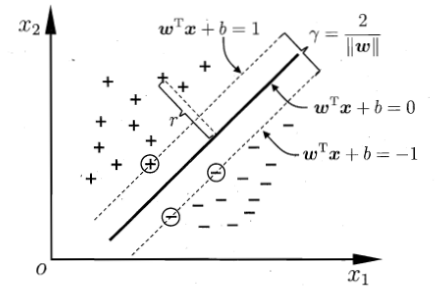
为了使得间隔最大,也就是求$\max\limits_{w,b} \frac{2}{\mid\mid \omega \mid\mid}$
转换为$\min\limits_{w,b}\frac{\mid\mid \omega \mid\mid^2}{2}$
这就是支持向量机
对偶问题
模型$f(x)=\vec{\omega}^T \vec{x}+b$,参数$\omega b$是模型参数。而$\min\limits_{w,b}\frac{\mid\mid \omega \mid\mid^2}{2}$是一个凸二次规划,除了使用现成的优化计算包外,我们可以使用数学上的对偶关系更高效的求出结果。
对这个凸二次规划式子添加拉格朗日乘子$\alpha \geq 0$,则问题的拉格朗日函数可写为:
$L(\vec{\omega},b,\vec{\alpha})=\frac{1}{2}\mid\mid \omega \mid\mid^2+\sum\limits_{i=1}^m\alpha_i(1-y_i(\omega^Tx_i+b))$
令L对$\omega b$的偏导为零可得:
$\omega=\sum\limits_{i=1}^m \alpha_iy_ix_i$
$0=\sum\limits_{i=1}^m\alpha_iy_i$
式1代入拉格朗日式子,式2作为约束函数,得到上一小节式子的对偶问题:
$\max\limits_{\alpha} \sum_{i=1}^m\alpha_i-\frac{1}{2}\sum_{i=1}^m\sum_{j=1}^m \alpha_i \alpha_j y_i y_jx_i^T x_j$
约束条件:$\sum\limits_{i=1}^m\alpha_iy_i=0$
上式是南教授《机器学习》书中记录的式子,这里认为下面式子可能更好理解
$\max\limits_{\alpha} \sum_{i=1}^m\alpha_i+\frac{1}{2}\sum_{i=1}^m\sum_{j=1}^m \alpha_i \alpha_j y_i y_jx_i^T x_j$
从上式解出$\vec{\alpha}$之后,求出$\vec{\omega}$和b即可得到模型:
$f(\vec{x})=\vec{\omega}^T\vec{x}+b=\sum\limits_{i=1}^m \alpha_iy_ix_i^T\vec{x}+b$
支持向量机一个极其重要的特性就是:训练完成后,大部分的训练样本不需要保存,最终模型仅与支持向量有关。上式是一个二次规划问题,求解的高效办法是使用SMO。
使用SMO求解
SMO(Sequential Minimal Optimization)基本思路:固定$\alpha_i$之外的所有参数,然后求$\alpha_i$上的极值。
具体到这个问题,由于存在约束条件$\sum\limits_{i=1}^m\alpha_iy_i=0$,固定$\alpha$之外的值,则$\alpha$值都能导出。所以采用了部分的调整,每次固定两个变量$\alpha_i \alpha_j$之外的其余参数,之后不断执行下述步骤直到收敛:
选取一对需要更新的变量$\alpha_i \alpha_j$
固定其余参数,求解上个小结推导出的式子更新$\alpha_i \alpha_j$
对于两个需要更新参数$\alpha_i$和$\alpha_j$的选取,遵循一个规则,使选取的两变量所对应样本之间的间隔最大。
核函数
这个部分解决不能线性可分问题。
这类问题,一般是将样本从原始空间映射到更高维的特征空间,使得样本在高维度空间中线性可分。
引出
令$\phi(\vec{x})$表示将$\vec{x}$映射后的特征向量,于是在特征空间中划分超平面对应的模型可以表示为:
$f(\vec{x})=\omega^T \phi(\vec{x})+b$
类似在线性可分情况下的式子:
$\min\limits_{\vec{w},b} \frac{\mid\mid \vec{\omega} \mid\mid^2}{2}$
约束条件:
$y_i(\vec{\omega}^T \phi(x_i)+b) \geq 1, i=1,2,…,m$
对偶问题:
$\max\limits_{\alpha} \sum\limits_{i=1}^m\alpha_i-\frac{1}{2}\sum\limits_{i=1}^m\sum\limits_{j=1}^m \alpha_i\alpha_jy_iy_j \phi(x_i)^T\phi(x_j)$
约束条件:$\sum\limits_{i=1}^m \alpha_i y_i =0$
关键问题$\phi(x_i)^T\phi(x_j)$是映射到特征空间之后的内积。由于维度太高不易计算,构造这样的函数:
$\kappa(\vec{x}_i,\vec{x}_j)=\langle \phi(x_i),\phi(x_j) \rangle = \phi(x_i)^T\phi(x_j)$
原式求解得到:
$f(\vec{x})=\vec{\omega}^T\phi(\vec{x})+b$
$=\sum\limits_{i=1}^m\alpha_iy_i\phi(x_i)^T\phi(x)+b$
$=\sum\limits_{i=1}^m\alpha_iy_i\kappa(x,x_i)+b$
这里的\kappa就是核函数。


核函数组合
- $\kappa_1$和$\kappa_2$都是核函数,则对于任意正数$\gamma_1$和$\gamma_2$的线性组合:$\gamma_1\kappa_1 + \gamma_2\kappa_2$
核函数的内积: $\kappa_1 \bigotimes \kappa_2(\vec{x},\vec{z})=\kappa_1(\vec{x},\vec{z})\kappa_2(\vec{x},\vec{z})$
对于任意函数$g(x)$,$\kappa(\vec{x},\vec{z})=g(x)\kappa_1(\vec{x},\vec{z})g(z)$
都是核函数
软间隔
为了缓解某些连核函数都无法有效处理的分类问题,需要允许SVM在一些样本上出错,即允许某些样本不满足约束$y_i(\vec{w}^Tx_i+b) \geq 1$,引入了软间隔概念。
优化目标可以修改为:
$\min\limits{\vec{\omega},b}\frac{\mid\mid \omega \mid\mid^2}{2}+C\sum\limits_{i=1}^m\ell_{0/1}(y_i(\vec{\omega}^Tx_i+b)-1)$
其中$C > 0$是一个常数,$\ell_{0/1}$是”0/1损失函数”
$\ell_{0/1}(z) = 1 if z<0 else 0$
当C无穷大时,所有样本均需要满足约束,等价于前面小结的式子;C为可数实数,则允许样本不满足约束
为了使得$\ell$容易求导,通常使用下面几个数学性质较好的式子替代:
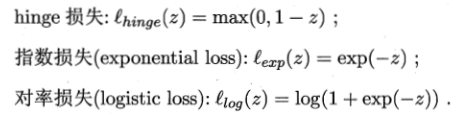
代入原式,然后使用松弛变量$\xi_i \geq 0$,松弛变量$\xi$替换原来C后面的部分,表示样本不满足约束的程度。
使用之前介绍的对偶问题求解出最终的答案。
支持向量回归
支持向量回归(Support Vector Regression)假设我们能够容忍f(x)与y之间最多有$\epsilon$的误差,即仅当f(x)与y之间差别的绝对值大于$\epsilon$时才算损失。
相当于以f(x)为中心,构建了一个宽度为$2\epsilon$的间隔带,落在带内的样本是正确的。

SVR问题可用式子表示:
$\min\limits{\vec{\omega},b}\frac{\mid\mid \omega \mid\mid^2}{2}+C\sum\limits_{i=1}^m\ell_{\epsilon}(f(x_i-y_i))$
其中$\ell_{\epsilon}$:$\ell_{\epsilon} ==0 if \mid z\mid \leq \epsilon else (\mid z \mid - \epsilon)$
引入松弛变量$\xi_{i}$和$\hat{\xi_{i}}$,原式重写为$\min\limits_{\vec{\omega},b,\xi_{i},\hat{\xi_{i}}}\frac{\mid\mid \vec{\omega}\mid\mid^2}{2}+C\sum\limits_{i=1}^m(\xi_{i} + \hat{\xi_{i}})$
引入拉格朗日乘子,求对偶问题
推导出带有核函数的算式
