临街小站

word2vec

发表于 | 分类于 | 阅读次数

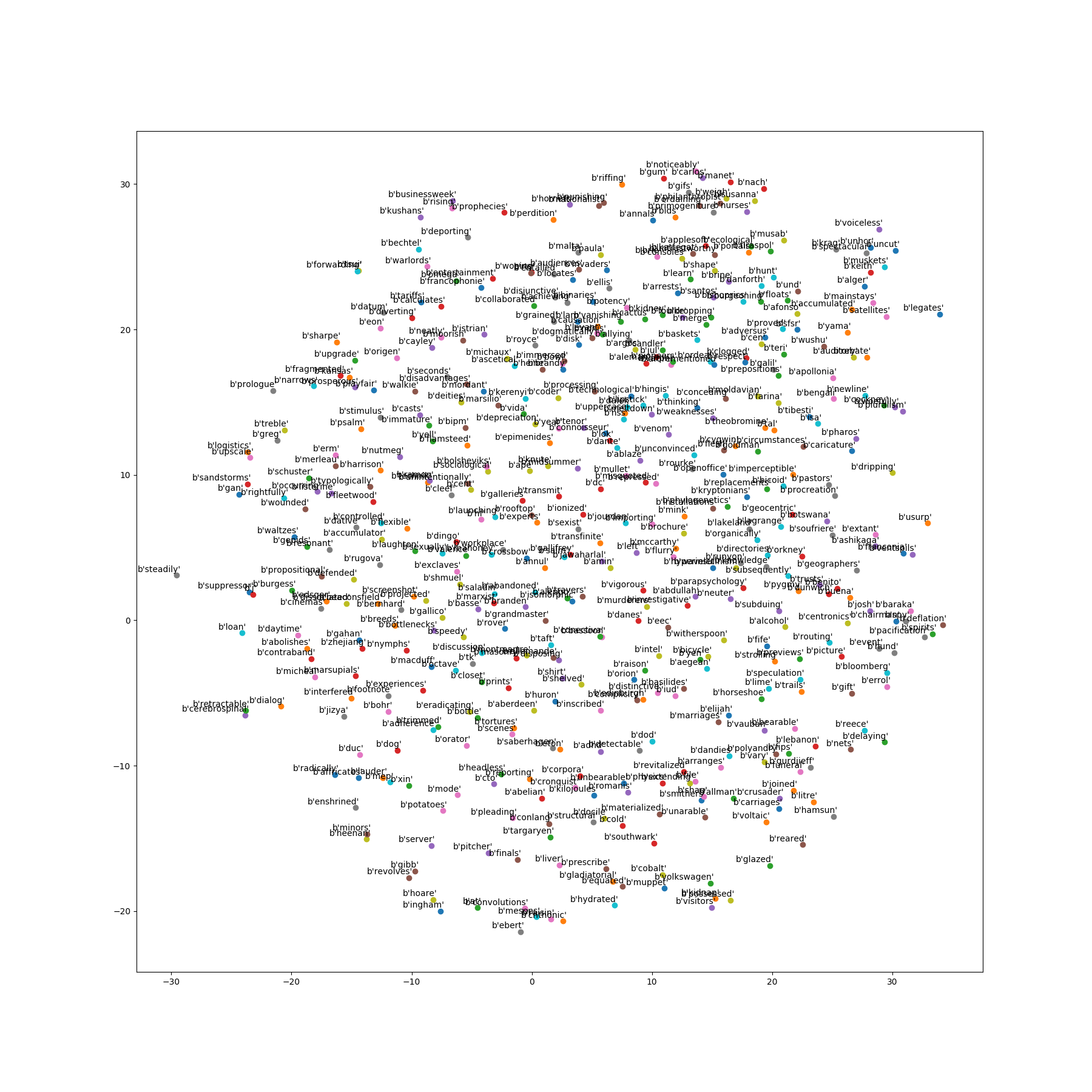
仅适用基于Hierarchical Softmax。

edit. 适用Negative Smapling

资源

word2vec通过训练将每个词映射成K维实数向量。通过词之间的距离，比如cosine相似度，欧式距离等来判断他们之间的语义相似度。根据词频使用哈弗慢编码，使得所有词频相似的词隐藏层的激活内容基本一致。出现频率越高的词语，他们激活的隐藏层数目越少，这样有效的降低了计算的复杂度。

用one-hot来通俗简单的理解，有三个词“麦克风”、“话筒”、“杯子”，用one-hot编码，三个词对应[1, 0, 0]， [0, 1, 0]，[0, 0, 1]。当成千上万的词语，会造成每个词向量含有很多0，也就是稀疏编码，所以我们需要降维。比如说，上面的三个词语可以表示为[0, 1]， [0.4, 0.9]，[1, 0]。这里要注意的是“麦克风”和“话筒”的意思很接近，所以它们对应的向量也很接近，即空间距离短，向量夹角小。

分布式假设，其核心思想为出现于上下文情景中的词汇都有相类似的语义。

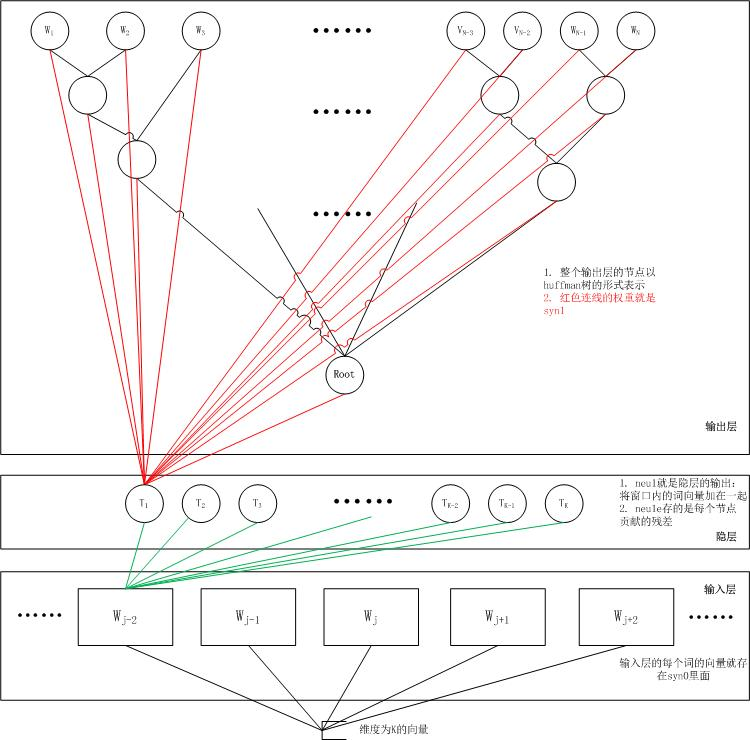
word2vec中用到的两个重要模型-CBOW（Continuous Bag-of-Words Model）模型和Skip-gram（Contunuous Skip-gram）模型。

两个模型都包含三层：输入层、投影层和输出层。前者是在已知当前词$w_t$的上下文$w_{t-2},w_{t-1},w_{t+1},w_{t+2}$的前提下预测当前词$w_t$，即$P(w_t \mid w_{t-2},w_{t-1},w_{t+1},w_{t+2})$；后者恰恰相反，在已知当前词$w_t$的前提下，预测上下文$w_{t-2},w_{t-1},w_{t+1},w_{t+2}$,也就是$P(w_{t-2},w_{t-1},w_{t+1},w_{t+2} \mid w_t)$

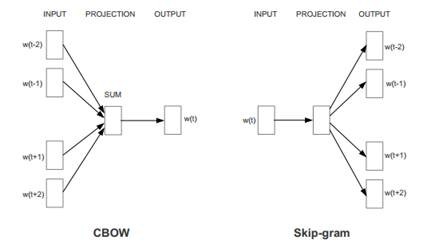
CBOW模型

CBOW模型包括三层：输入层投影层和输出层。


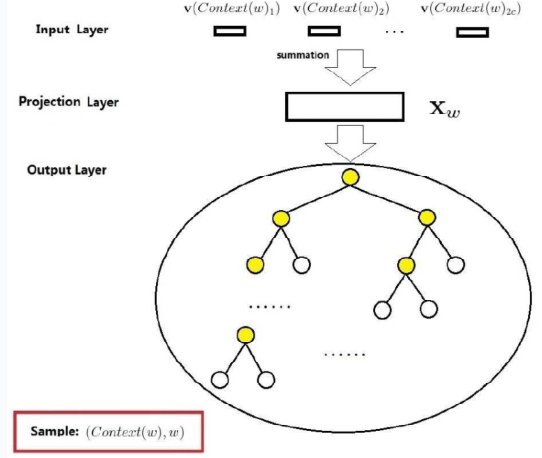
上面讲过CBOW模型网络结构是通过上下文context对当前词target做预测，求$P(w_t \mid w_{t-1},w_{t+1})$。

这里是假设Context(w)由w前后各c个词构成

  1. 输入层：包含Context(w)中2c个词的词向量$v(Context(w)_1),v(Context(w)_2),…,v(Context(w)_{2c})$，$Context(w) \in R^m$，这里，m的含义同上表示词向量的长度。

  2. 投影层：将输出层的2c个向量做求和累加，即$x_w=\sum_{i=1}^{2c}v(Countext(w)_i) \in R^m$

  3. 输出层：输出层对应一个二叉树，以语聊中出现的词当叶子节点，以各次在语聊中出现的次数当权值构造出来哈夫曼树。在哈夫曼树中，叶子节点一共$\mid D \mid$个，分别对应词典D中词，非叶子结点N-1个

取一个适当大小的窗口当做context window，输入层读入窗口内的词，将它们的向量（K维，初始随机）加和在一起，形成隐藏层K个节点。输出层是一个巨大的二叉树，叶节点代表语料里所有的词（语料含有V个独立的词，则二叉树有|V|个叶节点）。而这整颗二叉树构建的算法就是Huffman树。这样，对于叶节点的每一个词，就会有一个全局唯一的编码，形如”010011”，不妨记左子树为1，右子树为0。接下来，隐层的每一个节点都会跟二叉树的内节点有连边，于是对于二叉树的每一个内节点都会有K条连边，每条边上也会有权值。

对于语料库中的某个词$w_$t，对应着二叉树的某个叶子节点，因此它必然有一个二进制编码，如”010011”。在训练阶段，当给定上下文，要预测后面的词$w_t$的时候，我们就从二叉树的根节点开始遍历，这里的目标就是预测这个词的二进制编号的每一位。即对于给定的上下文，我们的目标是使得预测词的二进制编码概率最大。形象地说，我们希望在根节点，词向量和与根节点相连经过logistic计算得到bit=1的概率尽量接近0，在第二层，希望其bit=1的概率尽量接近1，这么一直下去，我们把一路上计算得到的概率相乘，即得到目标词$w_t$在当前网络下的概率$P(w_t\mid w_{t-1},w_{t+1})$。显而易见，按照目标词的二进制编码计算到最后的概率值就是归一化的.

模型的目标式子$p(w \mid Context(w))=\prod\limits_{j=2}^N p(d_j^w \mid x_w,\theta_{j-1}^w)$,用SGD训练优化模型，过程中更新相关的参数值（输入之后的加和向量值$x$，哈夫曼树中的内部节点向量$\theta$,以及原始的输入context中的所有向量参数$w$），每次取出一个样本$(context(w),w)$做训练，就要对整体的参数进行更新一次。对于$\theta$和$x$的值，通过SGD求偏导更新，而没有直接参与训练预测的原始context输入词向量$w$，我们通过$x$这个所有context词的加和向量来更新词向量$w$。把梯度贡献的更新项分配到所有输入中。

Skip-gram

Skip-Gram模型采取CBOW的逆过程的动机在于：CBOW算法对于很多分布式信息进行了平滑处理（例如将一整段上下文信息视为一个单一观察量）。很多情况下，对于小型的数据集，这一处理是有帮助的。相形之下，Skip-Gram模型将每个“上下文-目标词汇”的组合视为一个新观察量，这种做法在大型数据集中会更为有效。

Skip-gram模型包括两层：输入层和输出层，相比CBOW，少了投影层，因为它不需要对所有的context词进行特征向量相加。

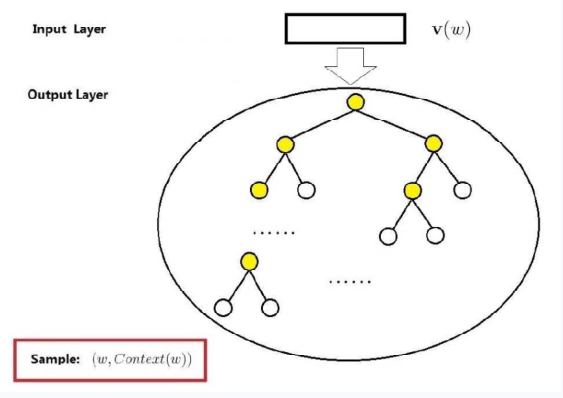
  1. 输入层：目标词的词向量$v(w) \in R^m$

  2. 输出层：与CBOW类似，输出层十一颗哈夫曼树

大体上来讲，Skip-Gramm与CBOW的流程相反，通过目标词对context进行预测，Skip-Gramm将其定义为$p(Context(w)\mid w)=\prod\limits_{w \in Context(w)} p(u \mid w)$，而上市中的$p(u \mid w)$可以按照上面的思想，通过哈夫曼树的路径节点乘积确定：$p(u \mid w)=\prod\limits_{j=2}^{l^u} p(d_j^u \mid v(w),\theta_{j-1}^u)$

之后就是对公式进行MLE的SGD优化。要注意的是，因为这里是要对context词进行预测，所以要从哈夫曼树的根部到叶子结点，进行$\mid context \mid$次。每次预测之后，都要处理完一个Context中的一个词之后，就要更新输入词的特征向量。

下面开始介绍基于Negative Smapling的模型，翻译过来就是负采样模型，是由NCE（Noise Contrastive Estimation）的一个简化版本，目的是用来提高训练速度并改善词向量的质量。与上面介绍的基于Hierarchical Softmax的CBOW和Skip-gram相比，这种不使用复杂的哈夫曼树，而使用相对简单的随机负采样。因为在计算损失函数的时候，只是有我们挑选出来的k个noise word，而非整个的语料库V，这使得训练非常快。大幅度提高性能。

假设要求的未知的概率密度函数为X，已知的概率密度是Y，如果知道了X与Y的关系，那么X也就可以求出来。本质就是利用已知的概率密度估计未知的概率密度函数。

负采样

算法主要讲对于一个给定的词w，如何生成$NEG(w)$。

词典$D$中的词在语料$C$中出现的次数有高有低，高频词应该被选为负样本的概率应该高点，低的反之，本质上是一个带权采样，这就是大体的要求。

记$l_0=0,l_k=\sum\limits_{j=1}^k len(w_j),k=1,2,3…,N$，这里$w_j$表示词典D中的第j个词，则以${l_j}^N_{j=0}$为部分节点可得到区间$[0,1]$上的一个等距划分，$I_i=(l_{i-1},l_i],i=1,2,…,N$为N个剖分区间。

进一步的引入区间$[0,1]$上的等距离剖分，剖分节点为${m_j}_{j=0}^M$，其中$M > > N$

将内部剖分节点${m_j}^{M-1}_{j=1}$投影到非等距剖分上，则可建立${m_j}^{M-1}_{j=1}$与区间${I_j}^N_{j=1}$的映射关系。之后每次生成一个$[1,M-1]$间的堆积整数r，通过映射关系就能确定选择那个词作负样本。注意万一选中的就是w自己，则跳过。

基于负采样的CBOW

在CBOW模型中，一直词w的上下文Context(w)，需要预测w，因此对于给定的Countext(w)，词w就是一个正样本，其他词就是负样本（分类问题）。

假定现在选好了关于Countext(w)的负采样集$NEG(w) \neq \emptyset$，并且
$$L^w(\hat{w})=
\begin{cases}
1,\hat{w}=w;\0,\hat{w}=w
\end{cases}
$$

表示词$\hat{w}$的标签，即正样本的标签为1，负样本的标签为0.

对于一个给定的正样本（Context（w）,w），我们希望最大化$$g(w)=\prod_{u \in {w} \bigcup NEG(w)} p(u \mid Context(w))$$

其中
$$p(u\mid Context(w))=
\begin{cases}
\sigma(x^T_w\theta^u),\ \ L^w(u)=1;\ \ 1-\sigma(x^T_w\theta^u), \ \ L^w(u)=0
\end{cases}
$$

这里$x_w$表示Context(w)中各词的词向量之和，而$\theta^u \in R^m$表示词u对应的一个辅助向量，其实就是word-embeding中的嵌入值。

$\sigma(x_w^T \theta^w)$表示当上下文为Context(w)时，预测中心词为w的概率，而$\sigma(x^T_w\theta^u)\, u \in NEG(w)$则表示上下文为Context(w)时，预测中心词为u的概率。式子$g(w)$表示，所有在NEG集合加上实际的中心词w概率相乘，最大化这个式子，每一项，如果是实际的中心词w，最大化$p$，如果属于NEG集合，最大化$(1-p)$。增大正样本的概率同时降低负样本的概率。

之后的内容就是使用SGD对求解最大化这个公式进行训练，参数的更新，包括$\theta$对应词的嵌入，$x$对应Context(w)中各词的词向量之和，以及通过$x$更新最初的输入词$w$的向量，对于整个数据集，当梯度下降的过程中不断地更新参数，对应产生的效果就是不断地移动每个单词的嵌套向量，直到可以把真实单词和噪声单词很好得区分开。

基于负采样的Skip-gram

对于一个给定的样本$(w,Context(w))$，我们希望最大化$$g(w)=\prod\limits_{\hat{w} \in Context(w)}\prod\limits_{u \in {w} \bigcup NEG^{\hat{w}}(w)} p(u\mid \hat{w})$$

其中$$p(u\mid \hat{w})=\begin{cases}\sigma(v(\hat{w})^T\theta^u, \ \ L^w(u)=1; \ \1-\sigma(v(\hat{w})^T\theta^u, \ \ L^w(u)=0 \end{cases}$$

这里$NEG^{\hat{w}}(w)$表示处理词$\hat{w}$时候生成的负样本子集，于是对于一个给定的语料库C，函数$$G=\prod\limits_{w\in C}g(w)$$
作为整体优化的目标，然后为了变成和项，我们取对数等等。

之后的步骤就跟原来一样。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
from __future__ import print_function
import tensorflow.python.platform

import collections
import math
from six.moves import xrange
import numpy as np
import os
import random
import tensorflow as tf
import urllib.request
import zipfile

# Step 1: Download the data.
url = 'http://mattmahoney.net/dc/'

def maybe_download(filename, expected_bytes):
  """Download a file if not present, and make sure it's the right size."""
  if not os.path.exists(filename):
    filename, _ = urllib.request.urlretrieve(url + filename, filename)
  # 文件信息获取
  statinfo = os.stat(filename)
  if statinfo.st_size == expected_bytes:
    print('Found and verified', filename)
  else:
    print(statinfo.st_size)
    raise Exception(
        'Failed to verify ' + filename + '. Can you get to it with a browser?')
  return filename

filename = maybe_download('text8.zip', 31344016)


# Read the data into a string.
def read_data(filename):
  f = zipfile.ZipFile(filename)
  # 获取压缩文件中的文件列表，返回第一个文件内容，根据空格进行分割成列表。
  for name in f.namelist():
  	return f.read(name).split()
  f.close()

words = read_data(filename)
print('Data size', len(words))

# Step 2: Build the dictionary and replace rare words with UNK token.#将稀少的词使用UNK替换
vocabulary_size = 50000

def build_dataset(words):
  count = [['UNK', -1]]# 词'UNK'代表UnKnow
  # 将count扩展，使用collections模块的计数器，根据出现次数的多少进行排序然后填充进count，排序之后UNK为第一位。s.most_common(n)方法返回对象s的Top n数据，没有指定的话，返回全部
  count.extend(collections.Counter(words).most_common(vocabulary_size - 1))
  dictionary = dict()
  for word, _ in count:#count中按item有两个内容：str以及对应的times频率。定义一个字典对象，键为str，对应的值为上面count中按str频率高低的排名例如 the:1,of:2。。。
    dictionary[word] = len(dictionary)
  data = list()
  unk_count = 0
  for word in words:
    if word in dictionary:
      index = dictionary[word]
    else:
      index = 0  # dictionary['UNK'] 注意之前在dictionary中根据排序，UNK还是在第一位，对应的值为0
      unk_count = unk_count + 1
    # index代表了词对应的排名，出现一次，填充进data中一次。data中包含的是原来文件中词对应的排名列表
    data.append(index)
  count[0][1] = unk_count # count是一个二维的元祖，一个元素是'UNK':times，count[0][1]代表的就是UNK对应的频率
  reverse_dictionary = dict(zip(dictionary.values(), dictionary.keys()))#键值对reverse
  return data, count, dictionary, reverse_dictionary

data, count, dictionary, reverse_dictionary = build_dataset(words)
del words  # Hint to reduce memory.
print('Most common words (+UNK)', count[:5])# 输出频率最高的5个词
print('Sample data', data[:10])

data_index = 0


# Step 4: Function to generate a training batch for the skip-gram model.
# num_skips 训练样本的源端要使用几次，出于n-skip算法的原因，一个中心词要对应多个周边词，也就是说一个中心词target要预测几次周边词，对应的词的数量
# skip_window 左右各考虑多少个词，skip_windows*2=num_skips
def generate_batch(batch_size, num_skips, skip_window):
  global data_index
  assert batch_size % num_skips == 0
  assert num_skips <= 2 * skip_window
  # ndarray本质是数组，其不同于一般的数组，或者Python 的list的地方在于它可以有N 维（dimentions），也可简单理解为数组里面嵌套数组。
  batch = np.ndarray(shape=(batch_size), dtype=np.int32)
  labels = np.ndarray(shape=(batch_size, 1), dtype=np.int32)
  span = 2 * skip_window + 1 # [ skip_window target skip_window ]
  buffer = collections.deque(maxlen=span)
  for _ in range(span):
    # 最初的填充，填充进原来文本中word的频率
    buffer.append(data[data_index])
    # 因为data_index是全局变量，训练要很多步，后面取余
    data_index = (data_index + 1) % len(data)
  for i in range((int)(batch_size / num_skips)):#batch中样batch_size个样本，衣蛾target有num_skips个样本
    target = skip_window  # target label at the center of the buffer
    targets_to_avoid = [ skip_window ]
    for j in range(num_skips):
      while target in targets_to_avoid:
        # 进行了num_skips轮，每次找到一个不在target_to_avoid中的元素，实际上就是每次找一个与target配对的word
        target = random.randint(0, span - 1)
      targets_to_avoid.append(target)
      batch[i * num_skips + j] = buffer[skip_window] #batch中是连续的num_skips个target词
      labels[i * num_skips + j, 0] = buffer[target]#label中连续的num_skip个周边词
    buffer.append(data[data_index])#buffer是有容量限制的，之前的状态是满的，此时会将最早的元素挤出去
    data_index = (data_index + 1) % len(data)
  return batch, labels

batch, labels = generate_batch(batch_size=8, num_skips=2, skip_window=1)
for i in range(8):
  print(batch[i], '->', labels[i, 0])
  print(reverse_dictionary[batch[i]], '->', reverse_dictionary[labels[i, 0]])

# Step 5: Build and train a skip-gram model.

batch_size = 128
embedding_size = 128  # 嵌入矩阵的密度，或者说是矩阵长度，batch_size要和embedding_size一致
skip_window = 1       # How many words to consider left and right.
num_skips = 2         # How many times to re-use an input to generate a label.


# 构造NEG集合相关参数，集合中的元素就作为分类结果的干扰
valid_size = 16     # Random set of words to evaluate similarity on.#随机的word集合估计相似度
valid_window = 100  # 选择在头部分布的开发样本
valid_examples = np.array(random.sample(xrange(valid_window), valid_size))# 从[0,valid_window]中随机的获取valid_size个数值返回
num_sampled = 64    # 负采样的个数

graph = tf.Graph()

with graph.as_default():

  # Input data.
  train_inputs = tf.placeholder(tf.int32, shape=[batch_size])
  train_labels = tf.placeholder(tf.int32, shape=[batch_size, 1])
  valid_dataset = tf.constant(valid_examples, dtype=tf.int32)

  # Construct the variables.
  embeddings = tf.Variable(#使用唯一的随机值来初始化大矩阵，shape=[vocabulary_size, embedding_size]
      tf.random_uniform([vocabulary_size, embedding_size], -1.0, 1.0))
  nce_weights = tf.Variable(#每个word定义一个权重值与偏差
      # tf.truncated_normal初始函数将根据所得到的均值和标准差，生成一个随机分布。shape=[vocabulary_size, embedding_size]
      tf.truncated_normal([vocabulary_size, embedding_size],
                          stddev=1.0 / math.sqrt(embedding_size)))
  nce_biases = tf.Variable(tf.zeros([vocabulary_size]))

  # Look up embeddings for inputs. 根据train_inputs中的id，寻找embeddings中的对应元素。比如，train_inputs=[1,3,5]，则找出embeddings中下标为1,3,5的向量组成一个矩阵返回。
  embed = tf.nn.embedding_lookup(embeddings, train_inputs)#这里是从train_inputs给的索引值找到embeddings大矩阵中的对应的嵌入值

  # Compute the average NCE loss for the batch.
  # tf.nce_loss automatically draws a new sample of the negative labels each
  # time we evaluate the loss.
  loss = tf.reduce_mean(# reduce_mean是平均值  vocabulary_size代表可能的数目  num_sampled代表per batch随机抽样的个数
      tf.nn.nce_loss(nce_weights, nce_biases, train_labels,embed,#这里的参数都是按batch计算的，而非具体的某个样本.同时要注意的是原文件中参数排序出错，这里修正
                     num_sampled, vocabulary_size))

  optimizer = tf.train.GradientDescentOptimizer(1.0).minimize(loss)

  # 计算在minibatch和所有的embedding的cosine相似度
  norm = tf.sqrt(tf.reduce_sum(tf.square(embeddings), 1, keep_dims=True))#tf.reduce_sum就是求和
  normalized_embeddings = embeddings / norm# 正则化嵌入值
  valid_embeddings = tf.nn.embedding_lookup( #NEG集嵌入值
      normalized_embeddings, valid_dataset)#寻找NEG集合中对应的正则化后的嵌入值
  similarity = tf.matmul(#NEG集合正则化后的嵌入值与词典集合正则化后的嵌入值的矩阵乘
      valid_embeddings, normalized_embeddings, transpose_b=True)

# Step 6: Begin training
num_steps = 100001

with tf.Session(graph=graph) as session:
  # We must initialize all variables before we use them.
  tf.initialize_all_variables().run()
  print("Initialized")

  average_loss = 0
  for step in xrange(num_steps):
    batch_inputs, batch_labels = generate_batch(
        batch_size, num_skips, skip_window)
    feed_dict = {train_inputs : batch_inputs, train_labels : batch_labels}

    # We perform one update step by evaluating the optimizer op (including it
    # in the list of returned values for session.run()
    _, loss_val = session.run([optimizer, loss], feed_dict=feed_dict)
    average_loss += loss_val

    if step % 2000 == 0:
      if step > 0:
        average_loss = average_loss / 2000
      # The average loss is an estimate of the loss over the last 2000 batches.
      print("Average loss at step ", step, ": ", average_loss)
      average_loss = 0

    # 这里是构建nosie词作
    # 注意这里的代价是很大的，没500步差不多就会减慢20%的计算
    if step % 10000 == 0:
      sim = similarity.eval()
      for i in xrange(valid_size):
        valid_word = reverse_dictionary[valid_examples[i]]
        top_k = 8 # number of nearest neighbors#
        nearest = (-sim[i, :]).argsort()[1:top_k+1]# 返回的是按相似度排序后元素值的索引值
        log_str = "Nearest to %s:" % valid_word
        for k in xrange(top_k):
          close_word = reverse_dictionary[nearest[k]]
          log_str = "%s %s," % (log_str, close_word)
        print(log_str)
  final_embeddings = normalized_embeddings.eval()

# Step 7: Visualize the embeddings.

def plot_with_labels(low_dim_embs, labels, filename='tsne.png'):
  assert low_dim_embs.shape[0] >= len(labels), "More labels than embeddings"
  plt.figure(figsize=(18, 18))  #in inches
  for i, label in enumerate(labels):
    x, y = low_dim_embs[i,:]
    plt.scatter(x, y)
    plt.annotate(label,
                 xy=(x, y),
                 xytext=(5, 2),
                 textcoords='offset points',
                 ha='right',
                 va='bottom')

  plt.savefig(filename)

  try:
    from sklearn.manifold import TSNE
    import matplotlib.pyplot as plt

    tsne = TSNE(perplexity=30, n_components=2, init='pca', n_iter=5000)
    plot_only = 500
    low_dim_embs = tsne.fit_transform(final_embeddings[:plot_only,:])
    labels = list(dictionary.keys())[:plot_only]
    plot_with_labels(low_dim_embs, labels)

  except ImportError:
    print("Please install sklearn and matplotlib to visualize embeddings.")'''

运行结果如下：

clinjie wechat
Think about u every day