拉格朗日乘子法
拉格朗日乘子法(Lagrange multipliers)是一种寻找多元函数在一组约束下的极值的方法。通过引入拉格朗日乘子,可将有$d$个变量与$k$个约束条件的最优化问题转化为具有$d+k$个变量的无约束优化问题求解
基本的拉格朗日乘子法就是求函数$f(x_1,x_2,…)$在$g(x_1,x_2,…)=0$的约束条件下的极值的方法。主要思想是将约束条件与原函数联系在一起,使能配成与变量数量相等的等式方程,从而求得原函数极值的各个变量的解。
例子:假设需要求极值的目标函数为$f(x)$,约束条件为$\phi(x,y)=M$
设$g(x,y)=M-\phi(x,y)$,定义一个新函数$F(x,y,\lambda)=f(x,y)+\lambda g(x,y)$
求偏导:
$$
\begin{cases}
&\frac{\partial F}{\partial x}=0 \\
&\frac{\partial F}{\partial y}=0\\
&\frac{\partial F}{\partial \lambda}=0
\end{cases}
$$
求出$x,y,\lambda$的值,代入即可得到目标函数的极值。
机器学习中的拉格朗日乘子法,一般用于求解约束优化问题的方法,当目标函数是凸函数时,求解最小值,使用拉格朗日乘子法求得的局部最优解就是全局最优解。类似的,在凹函数中,求得的最大值,局部最大解就是全局最大解。
在没有约束条件下,直接使用求导取指即可,但是有了约束条件后,就不能这样任意的小了,需要首先满足约束条件之后再求解。
在二维空间中求解,假设约束条件是一个曲线: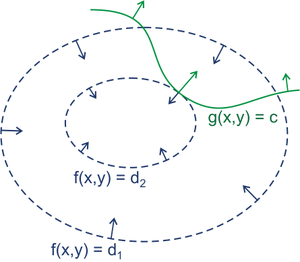
环线是目标函数的取值的等高线,需要紧贴约束线来满足约束条件求得理想值。
图中可以很清晰的看出来,与约束条件相切的等高线正合适。至于其他的与约束条件曲线相切的都不能考虑,因为这种取值一部分是符合约束条件的,一部分不能满足约束条件。
曲线相切,实际上就是法线向量平行,同方向或者反方向。最优解处,f和g的斜率平行。也就是说,存在一个非零实数与其中一个斜率相乘,等于另外一个曲线的斜率。这个实数称之为$\lambda$,或者$-\lambda$随便啦
$\nabla[f(x,y)+\lambda(g(x,y)-c)]=0$
一旦求出λ的值,将其套入下式,易求在无约束极值和极值所对应的点。
$F \left( x , y \right) = f \left( x , y \right) + \lambda \left( g \left( x , y \right) - c \right)$
新方程$F(x,y)$在达到极值时与$f(x,y)$相等,因为$F(x,y)$达到极值时$g(x,y)-c$总等于零。
定义拉格朗日函数:$L(x,\lambda)=f(x)+\lambda g(x)$ 将其对$x$的偏导数$\nabla_xL(x,\lambda)$置零即得式子$\nabla f(x)+\lambda g(x)=0$;同时对$\lambda$的偏导数$\nabla_{\lambda}L(x,\lambda)$置零即得约束条件$g(x)=0$。所以原约束问题转换成了对拉格朗日函数$L(x,\lambda)$的无约束优化问题。
KKT

现在考虑不等式$g(x) \leq 0$,如上图,此时最优点$x$或者在$g(x)<0$也就是环形区域内;或者在$g(x)=0$环形线上。
对于$g(x)<0$的情况,约束$g(x) \leq 0$不起作用,可以直接通过条件$\nabla f(x)=0$来获得最优点,这里等价于将$\lambda=0$之后求解$\nabla _x L(x,\lambda)=0$
$g(x)=0$的情况类似与上图左侧,但是有一些区别。在拉格朗日乘子中,约束条件$g(x)$与$f(x)$保持梯度平行即可,可就是说参数$\lambda$无关正负;到了这里,我们好好分析一下,假设两者的梯度是同方向的,都是向外(就是环线区域外,相反方向当然也可以)。我们都知道,函数是按沿着梯度方向增大,所以$f(x)$在区域外的值是大于区域内的值,也就是说,区域内的值是小值。我们的目标就是在约束条件下求$\min f(x)$,这里区域内是满足约束条件的,所以最优值显然不在环线上取,而是在区域内取。如果我们非要在环线上取怎么办?两个函数的梯度方向相反。这样才符合我们的认知嘛,梯度相反,同一个方向一个变小一个变大,环线是临界值,很符合人们的罗辑思维。
接着说不等式约束条件,整合上面的两种情况:
- $g(x)<0$,约束条件不起作用,使$\lambda=0$
- $g(x)=0$,约束条件使得$\lambda > 0$
所以必有$\lambda g(x)=0$
KKT条件推出来了:
$$
\begin{cases}
&g(x) \leq 0;\\
&\lambda \geq 0;\\
&\mu_jg_j(x)=0;\\
\end{cases}.
$$
推广
推广到多个约束,考虑有m个等式约束和n个不等式约束,优化问题
$$
\begin{cases}
&\min\limits_x f(x)\\
&s.t. h_i(x)=0 \ \ (i=1,…,m),\\
&g_j(x) \leq 0 \ \ (j=1,…,n).\\
\end{cases}
$$
引入拉格朗日乘子$\lambda=(\lambda_1,\lambda_2,…,\lambda_m)^T$和$\mu=(\mu_1,\mu_2,…,\mu_n)^T$,相应的拉格朗日函数为
$$
L(x,\lambda,\mu)=f(x)+\sum\limits_{i=1}^m\lambda_ih_i(x)+\sum\limits_{j=1}^n\mu_jg_j(x)
$$
引入的拉格朗日乘子条件与KKT条件为:
$$
\begin{cases}
&h_i(x)=0;\\
&\lambda_i \neq 0;\\
&g_j(x) \leq 0;\\
&\mu_j \geq 0;\\
&\mu_jg_j(x)=0.\\
&\end{cases}
$$
