主动学习与半监督
假设我们有训练样本集$D_l={ (x_1,y_1),(x_2,y_2),…,(x_l,y_l) }$,l个样本的类别标记已知,称为有标记(labeled);此外还有$D_u={ x_1,x_2,…,x_u },l \ll u$,这u个样本样本的类别标记未知,称为未标记的unlabeled样本。
若直接使用之前一直介绍的监督学习,则仅有$D_l$能用于构建模型,剩余的未标记样本都浪费了;另一方面远小于u数量的标记样本往往由于训练样本不足,学得模型的泛化能力往往不佳。
主动学习
一个做法是用$D_l$先训练一个模型,使用这个模型在$D_u$中拿一个模型出来,寻求专家知识,判定结果,然后把这个新标记的样本加入到$D_l$中重新训练一个模型,然后再去$D_u$中获取一个新的未标记样本。。。;如果每次都能挑出来对改善模型性能帮助大的瓜,则只需要询问专家较少的次数就能构建出较强的模型,大幅度的降低标记成本。称为主动学习(active learning),其目标是使用尽量少的查询获取尽量好的性能。
半监督学习
半监督(semi supervised)让学习器不依赖外界交互(针对主动学习的专家经验)、自动的利用未标记样本来提升学习性能。主要是考虑如何利用少量的标注样本和大量的未标注样本进行训练和分类。
半监督学习进一步可分为纯半监督学习和直推学习。前者假定训练数据中的未标记样本并非待预测的数据,而后者假定学习过程中所考虑的未标记样本是待预测数据,学习目的是在这些未标记样本上获得最优泛化能力。也就是说,纯半监督学习是基于开放世界,希望学得的模型能适用于训练过程中未观测带的数据;直推学习是基于封闭世界假设,仅试图对学习过程中观察到的未标记数据进行预测。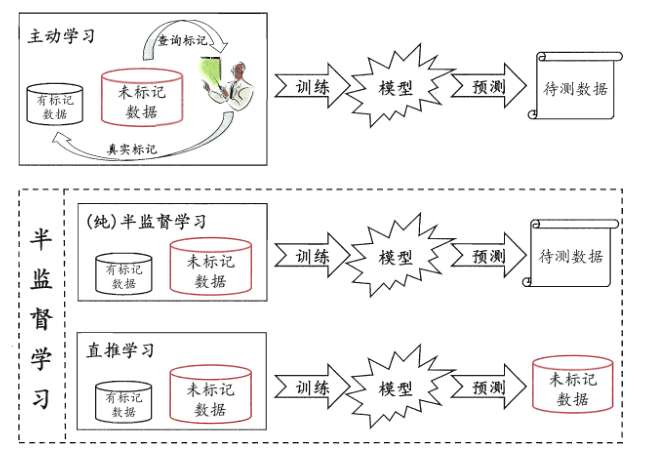
生成式方法
生成模型是半监督学习的一种模型,生成式方法是直接基于生成式模型的方法。此类方法假设所有数据(labeled、unlabeled)都是由同一个潜在的模型生成的,这个假设使得我们能够通过潜在模型的参数将未标记数据与学习目标联系起来,而未标记数据的标记则可看作模型的缺失参数,基于EM算法进行极大似然估计求解。
给定样本x,其真实类别标记为$y \in Y$,其中$Y = { 1,2,…,N }$为所有可能的类别。假设样本由高斯混合模型生成,且每个类别对应一个高斯混合成分:$p(x)=\sum\limits_{i=1}^N \alpha_i \cdot p(x \mid \mu_i,\sum_i)$
其中,混合系数$\alpha \geq 0,\sum_{i=1}^N \alpha_i=1;p(x \mid \mu_i,\sum_i)$是样本x属于第i个高斯混合成分的概率;$\mu_i$和$\sum_i$为该高斯混合成分的参数。
令$f(x) \in Y$表示模型f对x的预测标记,$\Theta \in { 1,2,…,N }$表示样本x隶属的高斯混合成分。由最大化后验概率可知:
$$
f(x)=arg \max\limits_{j \in Y} p(y= j \mid x)
=arg \max\limits_{j \in Y} \sum\limits_{i=1}^Np(y=j,\Theta=i \mid x)
=arg \max\limits_{j \in Y} \sum\limits_{i=1}^Np(y=j,\Theta=i,x)\cdot p(\Theta =i \mid x)
$$
其中$p(\Theta=i \mid x)=\frac{\alpha_i \cdot p(x \mid \mu_i,\sum_i)}{\sum\limits_{i=1}^N\alpha_i \cdot p(x \mid \mu_i,\sum_i)}$(不涉及样本标记)是样本x由第i个高斯混合成分生成的后验概率,$p(y=j \mid \Theta =i ,x)$是x由第i个高斯混合成分且类别为j的概率。
给定标记样本集$D_l={ (x_1,y_1),(x_2,y_2),…,(x_l,y_l) }$和未标记样本集合$D_u={ x_{l+1},x_{l+2},…,x_{l+u} },l \ll u l+u=m$假定所有样本独立同分布,且都是由同一个高斯混合模型生成。用极大似然估计法来估计高斯混合模型的参数,使用EM算法。
半监督SVM
半监督SVM(简称S3VM)是支持向量机在半监督学习上的推广,在不考虑未标记样本时,支持向量机试图找到最大间隔划分超平面,而在考虑未标记样本后,S3VM试图找能将两类有标记样本分开,且穿过数据低密度区域的划分超平面。
简单介绍一下其中最出名的TSVM,针对二分类问题,TSVM考虑对未标记样本进行各种可能的标记指派,然后再所有这些结果中寻求一个在所有样本(包括labeled and unlabeled)上间隔最大化的划分超平面。一旦划分超平面确定,未标记样本最终标记就是预测结果。
显然上面的思路是利用穷举方法,这样明显效率不高,TSVM在上面再进一步。给定$D_l={(x_1,y_1),(x_2,y_2),…,(x_l,y_l)}$和$D_u={x_{l+1},x_{l+2},…,x_{l+u}},y_i \in {-1,+1},l \ll u,l+u=m$。TSVM的学习目标就是为$D_u$中的样本给出预测标记$\hat{y}=(\hat{y}_{l+1},\hat{y}_{l+2},…,\hat{y}_{l+u}),\hat{y_i} \in {-1,+1}$,使得:$\min\limits_{\omega,b,\hat{y},\xi}\frac{1}{2}\mid\mid \omega \mid\mid_2^2+C_l\sum\limits_{i=1}^l \xi_i +C_u \sum\limits_{i=l+1}^m \xi_i$
上式中,$(\omega,b)$确定了一个划分超平面;$\xi$为松弛向量,$\xi_i(i=1,2,…,l)$对应于有标记样本,$\xi_i(i=l+1,l+2,…,m)$对应与未标记样本;$C_l,C_u$是由用户指定的用于平衡模型复杂度、有标记样本与未标记样本重要程度的这种参数。
它使用有标记样本学得一个SVM,然后使用这个SVM对未标记的数据进行标记指派,将SVM预测的结果作为伪标记赋予未标记样本。接下来TSVM找出两个标记指派为异类且很可能发生错误的未标记样本,交换标记,重新求得更新后SVM的划分超平面和松弛向量(在这一步中,因为SVM求得的伪标记往往是不准确的,所以需要设置好$C_l,C_u$,将$C_l$值大一点,标明有标记样本的作用更大);然后再找两个标记指派为异类且很可能发生错误的未标记样本,交换。。标记指派完成后逐渐提高未标记样本对优化目标的影响,进行下一轮标记指派调整。。直到$C_u=C_l$
图半监督
思想:相似或者相关联的顶点尽可能的赋予相同标记连接,以保证图的标记尽可能的平滑。相似性或者关系度越高,连接的权值越大。
定义相似矩阵$W=(w_{ij})_{(l+u)\times(l+u)},w_{ij}=exp(-\frac{\mid\mid x_i-x_j \mid\mid^2}{2\sigma^2})\ if\ e=(x_i,e_j) \in E\ else\ 0$其中$\sigma$是带宽系数,用于控制权值的减缓程度。$w_{ij}$随着欧式距离的增加会减少。
标记传递算法:已标记数据$Rightarrow$近邻未标记数据$Rightarrow$次级近邻未标记数据
协同训练
协同训练(co-training)使用多学习器,学习器之间的分歧对未标记数据的利用很重要。
一个数据对象往往同时拥有多个属性集,每个属性集构成一个视图。假设不同的试图有相容性,即其包含的关于输出空间的信息是一只的,当两个一起考虑就会有大概率使得与真实标记接近。不同视图信息的互补性会给学习器的构建带来很多便利。
协同训练正是使用了多视图的相容互补性,假设数据有两个充分且条件独立视图。充分是指每个视图都包含足以产生最优学习器的信息,条件独立则是指在给定类别的标记下两个视图独立。协同训练使用下面的策略使用未标记数据:首先在每个视图上基于有标记样本分别训练出一个分类器,然后让每个分类器分别去挑选自己最有把握的未标记样本赋予伪标记,并将伪标记样本提供给另一个分类器作为新增的有标记样本用于训练更新。。。之后就是不断的过程迭代,直到分类器不再更新。
协同学习也可以在单视图上使用,例如使用不同的学习方法、不同的数据采样、甚至不同的参数设置。
半监督聚类
聚类是一种典型的无监督学习任务,不过我们通常能够获取一些额外的信息:必连与勿连信息,即两个样本一定属于一个label、一定不属于一个label;第二种就是获得少量的有标记样本。
