k近邻学习

k近邻（k-Nearest Neighboor，KNN）是一种常用的监督学习方法：给定测试样本，基于某种距离距离度量找出训练集中与其最靠近的k个训练样本，然后基于这k个训练样本的信息对本样本进行预测。分类学习中通常使用投票法，少数服从多数；回归学习中则使用平均法。通常为了体现出靠近的距离指标，在分类学习与回归学习中使用加权法，越靠近样本的权值越大。

给定测试样本x，若其最近邻样本为z，则最近邻分类器出错的概率就是x与z类别标记不同的概率：$P(err)=1-\sum\limits_{c \in y}P(c \mid x)P(c \mid z)$

假设样本独立同分布，且对任意x和任意小正数$\delta$，在x附近$\delta$距离范围内找到一个训练样本z；令$c^T=arg \max\limits_{c \in y}P(c \mid x)$表示贝叶斯最优分类器的结果，有：

$$
P(err)=1-\sum\limits_{c \in y}P(c \mid x)P(c \mid z)
\approx1-\sum\limits_{c \in y}P^2(c \mid x)
\leq 1- P^2(c^T \mid x)
=(1+P(c^T \mid x))(1-P(c^T \mid x))
\leq 2 \times (1-p(c^T \mid x))
$$

可以看出，在这种理想条件下KNN分类器的泛化错误率不超过贝叶斯错误率的两倍。

降维

上面的讨论的基础是在足够小的距离内都有相邻的样本作为参考，考虑到做个属性（也就是多个维度）的情况，需要的合适的样本数量回事天文数字。高维度空间会给距离计算带来很大麻烦。

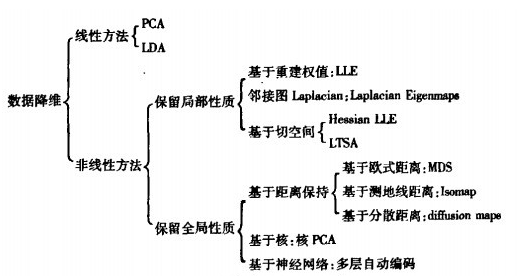
一般采用的方式是通过某种数学变换将原始高维属性空间转变为一个低维子空间。子空间中样本密度大幅提升。

MDS

MDS即多维缩放(Multiple Dimensional Scaling)，是要就将原始空间中样本间的距离在低维空间中得以保持。

假定m个样本在原始空间的距离矩阵为$D \in R^{m \times m}$，在第i行j列的元素$dist_{ij}$为样本$x_i$到$s_j$的距离。目标是获得样本在$d^c$维空间的表示$Z \in R^{d^c \times m},d^c \leq d$，且任意两个样本在$d^c$维空间的欧式距离等于原始空间$\mid\mid z_i-z_j \mid\mid = dist_{ij}$

令$B=Z^TZ \in R^{m \times m}$，其中B为降维后样本的内积矩阵，$b_{ij}=b_{ji}=z_i^Tz_j$

$$
dist_{i.}^2=\frac{1}{m}\sum\limits_{j=1}^m dist_{ij}^2
dist_{.j}^2=\frac{1}{m}\sum\limits_{i=1}^m dist_{ij}^2
dist_{..}^2=\frac{1}{m^2}\sum\limits_{i=1}^m\sum\limits_{j=1}^m dist_{ij}^2
$$

由以上的式子推出：

$b_ij=-\frac{1}{2}(dist_{ij}^2-dist_{i.}^2-dist_{.j}^2+dist_{..}^2)$

依次求出矩阵B中所有的元素，然后对矩阵做特征值分解：$B=V\Lambda V^T$其中V为特征向量矩阵，$\Lambda$为特征值构成的对角矩阵。假定其中有$d^c$个非零特征值，构成对角矩阵$\Lambda_x=diag(\lambda_1,\lambda_2,…,\lambda_{dx})$，令$Vx$表示相应的特征向量矩阵，则：

$Z=\Lambda_c^{1/2}V_c^T \in R^(d^c \times m)$

主成分分析

通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量，转换后的这组变量叫主成分。

主成份（Principal Component Analysis）分析是降维（Dimension Reduction）的重要手段。每一个主成分都是数据在某一个方向上的投影，在不同的方向上这些数据方差Variance的大小由其特征值（eigenvalue）决定。一般我们会选取最大的几个特征值所在的特征向量（eigenvector），这些方向上的信息丰富，一般认为包含了更多我们所感兴趣的信息。

在很多情形，变量之间是有一定的相关关系的，当两个变量之间有一定相关关系时，可以解释为这两个变量反映此课题的信息有一定的重叠。主成分分析是对于原先提出的所有变量，将重复的变量（关系紧密的变量）删去多余，建立尽可能少的新变量，使得这些新变量是两两不相关的，而且这些新变量在反映课题的信息方面尽可能保持原有的信息。

设法将原来变量重新组合成一组新的互相无关的几个综合变量，同时根据实际需要从中可以取出几个较少的综合变量尽可能多地反映原来变量的信息的统计方法叫做主成分分析或称主分量分析，是数学上用来降维的一种方法。

先定义一些变量：

样本$(\vec{x_1},\vec{x_2},\vec{x_3},…,\vec{x_m})$

投影变换得到的 新坐标系${ \vec{\omega_1},\vec{\omega_2},…,\vec{\omega_d}, }$

样本点在低维坐标系中的投影是$z_i=(z_{i1};z_{i2};z_{i3};…;z_{id_‘};)$

其中$z_{ij}=\vec{\omega}_j^T\vec{x_i}$是x在低维坐标系下的第j维坐标

投影点方差是$\sum_i W^Tx_ix_i^TW$ 优化目标是最大化这个方差，使得在投影之后尽可能的分散

PCA一般有以下几个步骤：

数据减去均值：样本中心化$\sum_i \vec{x_i}=\vec{0}$
计算协方差矩阵：$C=\frac{XX^T}{N}$
计算协方差矩阵的特征矢量和特征值：对协方差矩阵$\frac{XX^T}{N}$特征分解$CU=U\Lambda$，其中C为方差矩阵，U为计算的特征矢量，$\Lambda$是对角线矩阵$\Lambda=diag(\lambda_1,\lambda_2,…,\lambda_d)$
选择成分组成模式矢量对应最大特征值的特征矢量就是数据的主成分：取最大的d个特征值所对应的特征向量$u_1,u_2,…,u_d$

一般地，从协方差矩阵找到特征矢量以后，下一步就是按照特征值由大到小进行排列，这将给出成分的重要性级别。现在，如果你喜欢，可以忽略那些重要性很小的成分，当然这会丢失一些信息，但是如果对应的特征值很小，你不会丢失很多信息。

获得投影的新数据$y_i=U_k^T x_i$

核化线性降维

线性降维假设从高维空间到低维度空间的函数映射是线性的，然而在不少的现实任务中，可能需要非线性映射才能找到恰当的低维嵌入。

非线性降维的一种常用方法是基于核技巧对线性降维方法进行”核化”。

在KPCA中，除了在PCA中的一些先决条件外，我们认为原有的数据有更高的维数，我们可以在更高的维度空间中做PCA分析（即在更高维里，把原始数据向不同方向进行投影）

我们拿到样本点，需要将它映射到高维空间中，然后使用PCA算法进行降维。

假定我们将在高维特征空间中把数据投影到由W确定的超平面上，即PCA欲求解$(\sum\limits_{i=1}^m)\vec(W)=\lambda \vec{W}$ （拉格朗日乘子法）

其中$z_i$是样本点在高维特征空间的像，有$\vec{W}=\sum\limits_{i=1}^m z_i \alpha _i$

$\alpha_i=\frac{1}{\lambda}z_i^T \vec{W}$

z是由原始属性空间中的样本点x通过映射$\phi$产生。但是在映射到高维空间这一步，一般情况下，我们并不知道映射函数$phi$的具体形，不知道要映射到哪重维度上，于是引入核函数$\kappa(x_i,x_j)=\phi(x_i)^T\phi(x_j)$

化简式子：$KA=\lambda A$，K为$\kappa$对应核矩阵，$A=(\alpha_1;\alpha_2;…;\alpha_m)$

上式是特征值分解问题，取K对应的最大的d个特征值对应的特征向量。

对于新样本x，投影的第j维坐标为$z_j=\omega_j^T \phi(x)=\sum\limits_{i=1}^m \alpha_i^j \kappa(x_i,x)$

流形学习

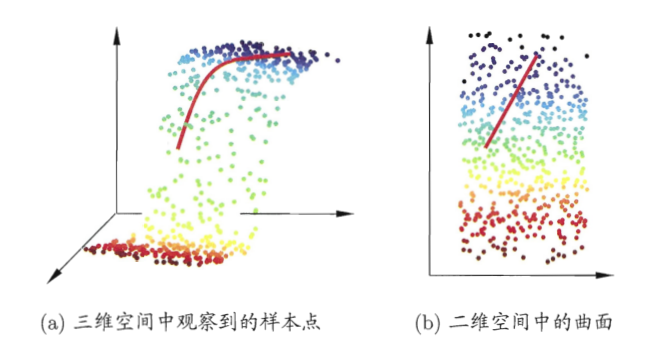
流形是一类借鉴了拓扑流形概念的降维方法，在局部有欧式空间的性质，能用欧式距离来进行距离计算。

若低维流形嵌入到高维空间中，则数据样本在高维空间的分布虽然看上去非常复杂，但在局部上仍具有欧式空间的性质。因此可以容易的在局部建立降维映射关系，然后再设法将局部映射关系推广到全局。

等度量映射

等度量映射（Isometric Mapping）认为低维流形嵌入到高维空间后，直接在高维空间中计算直线距离具有误导性，因为高维空间中的直线距离往往在低维嵌入流形上是不可达的。

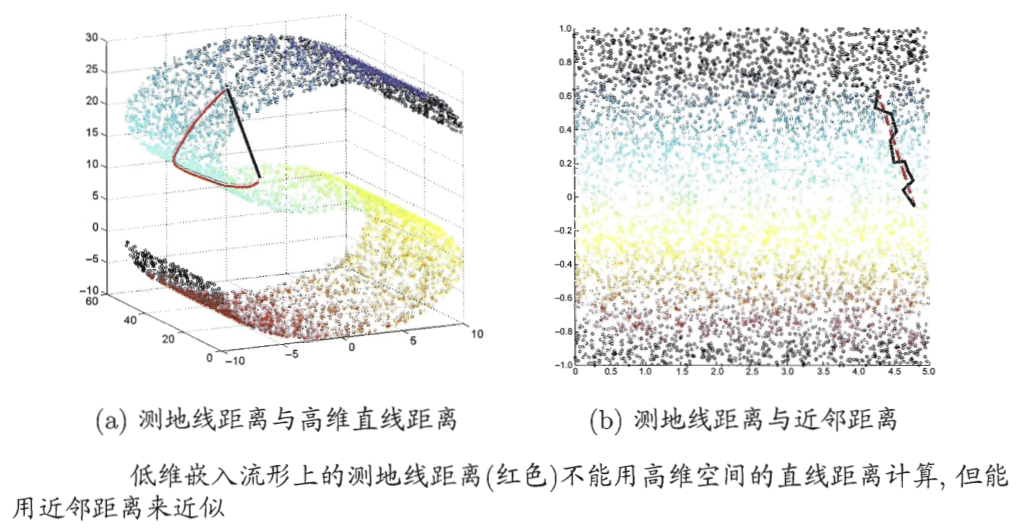
对每个点基于欧式距离找出其近邻点，然后就能建立一个近邻连接图，图中近邻点之间存在连接，而非近邻之间不存在连接，于是计算两点间测地线距离的问题，转变为了计算近邻点之间最短路径问题。

步骤：

确定$x_i$的k近邻，并将$x_i$与k近邻之间的距离设置为欧氏距离，与其他点的距离设置为无穷大
调用最短路径算法计算任意来那个样本之间的距离$dist(x_i,dist_j)$
将$dist(x_i,dist_j)$作为MDS算法的输入求解

局部线性嵌入

局部线性嵌入（Locally Linear Embedding，LEE）试图保持邻域内样本之间的线性关系。假定样本点$x_i$的坐标能通过他的邻域样本$x_j,x_k,x_l$的坐标通过线性组合组成，$x_i=w_{ij}x_j+w_{ik}x_k+w_{il}x_l$

LLE希望关系在低维空间中得以保持。

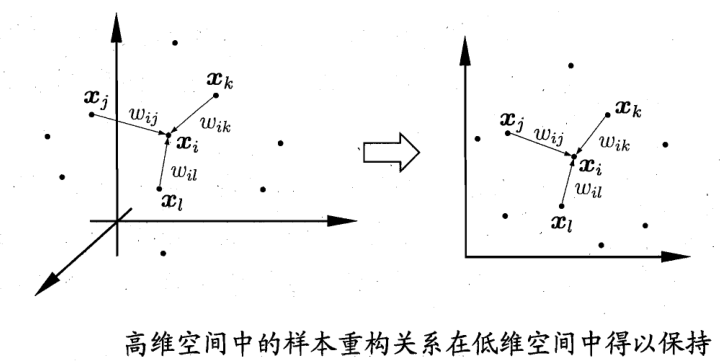
LLE算法的主要原理就是先在高维空间，计算出相应的重构系数序列$W={w_1,w_2,…,_m}$，随后在低维空间中通过相同的重构系数获取投影点。

令$Z=(z_1,z_2,…,z_m) \in R^{d^. \times m}$

$M = (I-W)^T(I-W)$则寻求最小化：$\min\limits_z tr(ZMZ^T)$，约束条件$ZZ^T=I$

上式通过特征值分解，M最小的$d^.$个特征值对应的特征向量组成的矩阵就是$Z^T$，即在低维的投影

度量学习

对两个d维样本$x_i x_j$，他们之间的平方欧式距离可写为：$dist^2(x_i,x_j)=dist_{ij,1}^2+dist_{ij,2}^2+…+dist_{ij,d}^2$

其中$dist_{ij,k}$表示$x_i,x_j$在第k维上的距离，若嘉定不同属性的重要程度不一样，可以引入属性权重$\omega$

$dist^2(w_i,x_j)=\omega_1\cdot dist_{ij,1}^2+\omega_2\cdot dist_{ij,2}^2+…+\omega_d\cdot dist_{ij,d}^2=(x_i-x_j)^T W(x_i-x_j)$

其中$\omega_i \geq 0,W=diag(\omega)$是一个对角矩阵

W是对角矩阵，坐标轴正交，属性之间无关；然而现实中并不是这样将W图换位一个普通的半正定对称矩阵M，得到马氏距离。

其中M称作“度量矩阵”，而度量学习是对M进行学习。M必须是正定对称的，即必有正交基P使得M能写成$M=PP^T$

对M的学习，我们需要把M直接嵌入到需要提高效率的评价指标中，通过优化指标求得M