机器学习可以根据样本是否有标签分类为有监督学习与无监督学习,前面介绍的基本都是有监督学习。无监督学习中,目标通过对无标记训练样本的学习来揭示数据的内在性质及规律。
聚类试图将数据集中的样本划分为若干个通常不相交的子集,每个子集称为一个簇(cluster)。通过这样的划分,每个簇可能对应与一些潜在的类别。这些类别两两不相交,并起来是整个数据集,聚类的结果就是产生一个标签结果序列。
性能度量
对聚类来讲,我们需要通过某种性能来评估聚类效果的好坏;若明确了最终要使用的性能度量,可以直接将其作为聚类过程的优化目标。
聚类性能度量大致有两类,一类是将聚类结果与某个参考模型进行比较,称为外部指标;另一类是直接考察聚类结果而不利用任何参考模型,称为内部指标。
外部指标
对数据集$D={x_1,x_2,…,x_m}$,假定通过聚类给出额簇划分为$C={C_1,C_2,…,C_k}$,参考模型给出的簇划分为$C^`={C_1^T,C_2^T,…,C_s^T}$。相应的,令$\lambda$与$\lambda^T$分别表示与C和$C^T$对应的簇标记向量。注意的是,参考模型给出的划分类别数量不一定等于通过聚类得到的数量。
样本两两配对:
$a=\mid SS \mid ,SS={(x_i,x_j)\mid \lambda_i = \lambda_j,\lambda_i^T=\lambda_j^T,i<j}$
$b=\mid SS \mid ,SD={(x_i,x_j)\mid \lambda_i = \lambda_j,\lambda_i^T\neq \lambda_j^T,i<j}$
$c=\mid SS \mid ,DS={(x_i,x_j)\mid \lambda_i \neq \lambda_j,\lambda_i^T=\lambda_j^T,i<j}$
$a=\mid SS \mid ,DD={(x_i,x_j)\mid \lambda_i \neq \lambda_j,\lambda_i^T \neq \lambda_j^T,i<j}$
集合SS包含了C中隶属于相同簇且在$C^`$中也隶属于相同簇的样本对,集合SD包含了在C中隶属于相同簇但在$C^T$中隶属于不同簇的样本对
Jaccard系数:$JC=\frac{a}{a+b+c}$
FM指数:$FMI=\sqrt{\frac{a}{a+b}\frac{a}{a+c}}$
Rand指数:$RI=\frac{2(a+d)}{m(m-1)}$
上述性能度量的结果值均在[0,1]区间,值越大越好。
内部指标
考虑聚类结果的簇划分$C={C_1,C_2,…,C_k}$,定义
$avg(C)=\frac{2}{\mid C \mid(\mid C \mid -1)}\sum_{1 \leq i < j \leq \mid C \mid}dist(x_i,x_j)$
$diam(C)=\max_{1 \leq i <j \leq \mid C \mid}dist(x_i,x_j)$;
$d_\min(C_i,C_j)=\min_{x_i \in C_i , x_j \in C_j} dist(x_i,x_j)$
$d_cen(C_i,C_j)=dist(\mu_i,\mu_j)$
上面的式子中,dist计算两个样本之间的距离;$\mu$代表簇的中心点$\mu=\frac{\sum_{1 \leq i \leq \mid C \mid x_i}}{\mid C \mid}$;avg(C)uiying与簇内样本间的平均距离,diam(C)对应与簇C内样本间的最远距离,$d_min(C_i,C_j)$对应与簇i和簇j最近样本间的距离;$d_{cen}(C_i,C_j)$对应与簇i和j中心点间的距离。
基于上面的指标,推出下面几个内部指标:
$DBI=\frac{1}{k}\sum\limits_{i=1}^k\max\limits_{j \neq i}(\frac{avg(C_i)+avg(C_j)}{d_{cen}(\mu_i,\mu_j)})$
$DI=\min\limits_{1 \leq i \leq k}{ \min\limits_{j \neq i}(\frac{d_{min}(C_i,C_j)}{\max_{1\leq l \leq k diam(C_l)}}) }$
显然,DBI的值越小越好,DI值越大越好
距离计算
在讨论距离计算的时候,属性是否定义了”序”关系很重要。例如定义域为${ 1,2,3 }$能直接在属性值上计算距离,这样的属性成为有序属性;而定义域为{ 飞机、火车、轮船 }这样的离散属性则不能直接在属性值上计算距离,称为无序属性。
对有序属性的距离计算,通常使用Minkowski distance:$dist_{mk}(x_i,x_j)=(\sum\limits_{u=1}^n \mid x_{iu}-x_{ju} \mid^p)^{\frac{1}{p}}$
对无需属性采用VDM算式:$VDM_p(a,b)=\sum\limits_{i=1}^k\mid \frac{m_{u,a,i}}{m_{u,a}}-\frac{m_{u,b,i}}{m_u,b} \mid ^p$
其中$m_{u,a} m_{u,a,i}$分别表示在属性u上取值a的样本数以及在第i个样本簇中属性u上取值为a的样本数。k为样本簇数
混合处理,假定有$n_c$个有序属性以及$n-n_c$个无序属性:
$MinkorDM_p(x_i,x_j)=(\sum\limits_{u=1}^{n_c}\mid x_{iu}-x_{ju} \mid ^p +\sum\limits_{u=n_c+1}^n VDM_p(x_{iu},x_{ju}))^{\frac{1}{p}}$
属性重要性不同时,可以加权处理
原型聚类
原型聚类算法假设聚类结构能够通过一组原型刻画,通常情况下算法先对原型进行初始化,然后对原型进行迭代更新。
k均值算法
给定样本集$D={x_1,x_2,…,x_m}$,k均值算法针对聚类所得簇划分${ C_1,C_2,…,C_k }$最小化平方误差。$E=\sum\limits_{i=1}^k\sum\limits_{x \in C_i}\mid\mid x-\mu_i \mid\mid_2^2$
其中$\mu_i=\frac{\sum_{x \in C_i}\vec{x}}{\mid C_i \mid}$是簇$C_i$的均值向量。上式在一定程度上刻画了簇内样本围绕簇均值向量的紧密吃呢孤独,E值越小则簇内样本相似度越高。k均值采用贪心策略,通过迭代优化来近似求解上式。
学习向量量化
学习向量量化(LVQ)试图找到一组原型向量来刻画聚类结构,它假设数据样本带有类别标记,学习过程利用样本的这些监督信息来辅助聚类。
算法首先对原型向量进行优化,然后对原型向量进行迭代优化。在每一轮的迭代中,算法随机选取一个有标记训练样本,找出与其距离最近的原型向量,并根据两者的类别标记是否一致来对原型向量进行更新。
在更新原型向量上,对样本$x_i$,若最近的原型向量$p_i$与$x_j$的类别标记相同,则令$p_i$向$x_j$方向靠拢;否则更新原型向量与$x_j$之间距离增大,远离$x_j$
高斯混合聚类
统计学习的模型有两种,一种是概率模型,一种是非概率模型。所谓概率模型,是指训练模型的形式是P(Y|X)。输入是X,输出是Y,训练后模型得到的输出不是一个具体的值,而是一系列的概率值(对应于分类问题来说,就是输入X对应于各个不同Y(类)的概率),然后我们选取概率最大的那个类作为判决对象(软分类–soft assignment)。所谓非概率模型,是指训练模型是一个决策函数Y=f(X),输入数据X是多少就可以投影得到唯一的Y,即判决结果(硬分类–hard assignment)。
高斯混合模型GMM就是指对样本的概率密度分布进行估计,而估计采用的模型(训练模型)就是几个高斯模型的加权和。每个高斯模型代表一个聚类。对样本中的数据分别在几个高斯模型上进行投影,就会分别得到在各个类上的概率,选取概率最大的类作为判决结果。
理论上可以通过增加模型的数量,用GMM近似任何概率分布
混合高斯模型定义:$p(x)=\sum_{k=1}^k \pi_kp(x \mid k)$
其中k为模型的个数;$\pi_k$为第k个高斯的权重;$p(x\mid k)$则为第k个高斯概率密度,其均值为$\mu_k$,方差为$\theta_k$。对此概率密度的估计就是要求出$\pi_k,\mu_k,\theta_k$。当求出p(x)的表达式后,求和式的各项的结果就分别代表样本x属于各个类的概率。
在做参数估计的时候,常采用的是最大似然方法。最大似然法就是使样本点在估计的概率密度函数上的概率值最大。由于概率值一般都很小,N 很大的时候, 连乘的结果非常小,容易造成浮点数下溢。所以我们通常取log,将目标改写成:$\max\sum\limits_{i=1}^N log(\sum\limits_{k=1}^K\pi_kN(x_i \mid \mu_k,\theta_k))$
一般用来做参数估计的时候,我们都是通过对待求变量进行求导来求极值,在上式中,log函数中又有求和,你想用求导的方法算的话方程组将会非常复杂,没有闭合解。可以采用的求解方法是EM算法——将求解分为两步:第一步,假设知道各个高斯模型的参数(可以初始化一个,或者基于上一步迭代结果),去估计每个高斯模型的权值;第二步,基于估计的权值,回过头再去确定高斯模型的参数。重复这两个步骤,直到波动很小,近似达到极值(注意这里是极值不是最值,EM算法会陷入局部最优)。具体表达如下:
E:对滴i个样本$x_i$来说,它由第k个模型生成的概率为:$\vec{w_i}(k)=\frac{\pi_kN(x_i \mid \mu_k,\theta_k)}{\sum\limits_{j=1}^K \pi_jN(x_i \mid \mu_j,\theta_j)}$
在这一步,假设高斯模型的参数是已知的,有上一步迭代而来或者由初始值决定
M:得到每个点的生成概率以后,对样本$x_i$来说,他的$\vec{w}_i(k)x_i$的值是由第k个高斯模型产生的。换句话说,第k个高斯模型很产生了$\vec{w}_i(k)x_i(i=1……N)$这些数据。这样在估计第k个高斯模型参数时,我们就用$\vec{w}_i(k)x_i(i=1……N)$这些数据去做参数估计:
$\mu_k=\frac{\sum\limits_{i=1}^N \vec{w}_i (k)x_i}{N}$
$\theta_k=\frac{\sum\limits_{i=1}^N\vec{w}_i(k)(x_i-\mu_k)(x_i-\mu_k)^T}{N_k}$
$N_k=\sum\limits_{i=1}^N\vec{w}_i(k)$
重复E和M知道算法收敛
密度聚类
$\epsilon$邻域:对象O的是与O为中心,$\epsilon$为半径的空间,参数$\epsilon > 0$,是用户指定每个对象的领域半径值。
MinPts(领域密度阀值):对象的$\epsilon$邻域的对象数量。
核心对象:如果对象O的$\epsilon$邻域对象数量至少包含MinPts个对象,则该对象是核心对象。
直接密度可达:如果对象p在核心对象q的$\epsilon$邻域内,则p是从q直接密度可达的。
密度可达:在DBSCAN中,p是从q(核心对象)密度可达的,如果存在对象链$(p_1,p_2,…,p_n)$,使得$p_1=x_i,p_n=x_j$,且有$p_{i+1}$由$p_i$直接密度直达
密度相连:对$x_i$和$x_j$,若存在$x_k$使得$x_i,x_j$均由$x_k$密度可达,则两者密度相连。
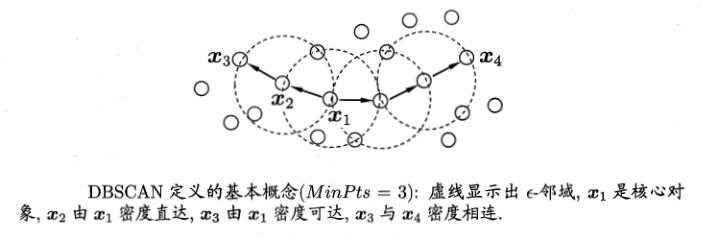
DBSCAN算法先任选数据集中的一个核心对象为种子,再由此出发确定相应的聚类簇。具体的,现根据给定的邻域参数$(\epsilon,MinPys)$找出所有的核心对象;然后以任意核心对象为出发点,找出由其密度可达的样本生成聚类簇,知道所有核心对象均被访问过为止。
层次聚类
层次聚类试图在不同层次对数据集进行划分,从而形成树形的聚类结构。数据集的划分可采用自底向上的聚合策略,也可选择自顶下下的分析策略。
AGNES是一种自底向上聚合策略的层次聚合算法。他先将数据集合中每个样本看作一个初始聚类簇,然后再算法运行的每一步中找出距离最近的两个聚类簇合并,该过程不断重复,直至达到预设的聚类簇个数。
算法的关键是如何找到最近的两个聚类簇,然后不断的进行合并。给定聚类簇$C_i$和$C_j$,通过下面的式子计算距离:
最小距离: $d_min(C_i,C_j)=\min\limits_{x \in C_,z \in C_j} dist(x,z)$
最大距离: $d_max(C_i,C_j)=\max\limits_{x \in C_,z \in C_j} dist(x,z)$
平均距离: $d_avg(C_i,C_j)=\frac{\sum\limits_{x \in C_i}\sum\limits_{z \in C_j}dist(x,z)}{\mid C_i \mid \mid C_j \mid}$
当使用不同的距离公式作为算法的因数时,算法分别被称为单链接,全连接以及均链接。算法首先对仅含一个样本样本的初始聚类簇和相应的距离矩阵进行初始化;然后不断合并距离最近的聚类簇,并对合并得到的新聚类簇距离矩阵进行更新;不断重复,直到聚类簇数量减少到预设目标。
